English

URL: https://ctf.hsctf.com/

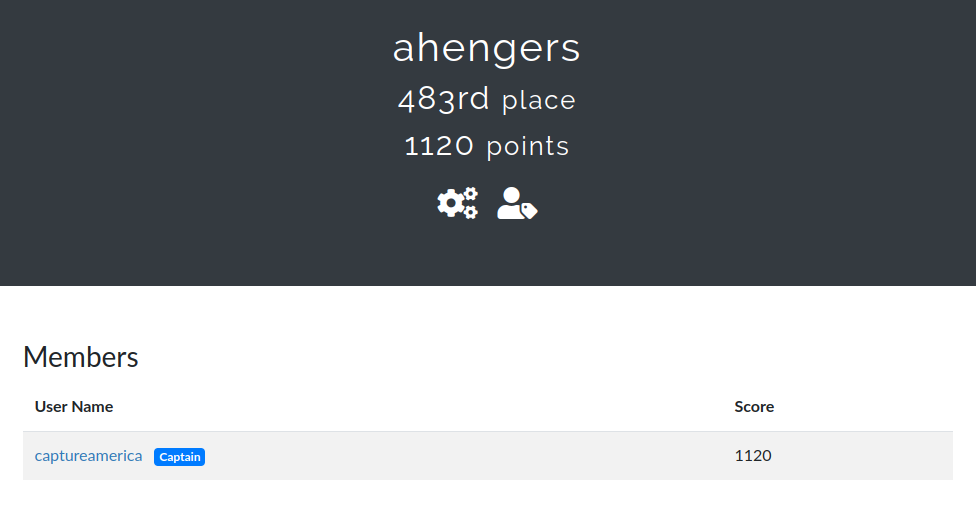
483位でした。ここ最近、簡単なのしか解けてません。。

hsctf7_Score1.png

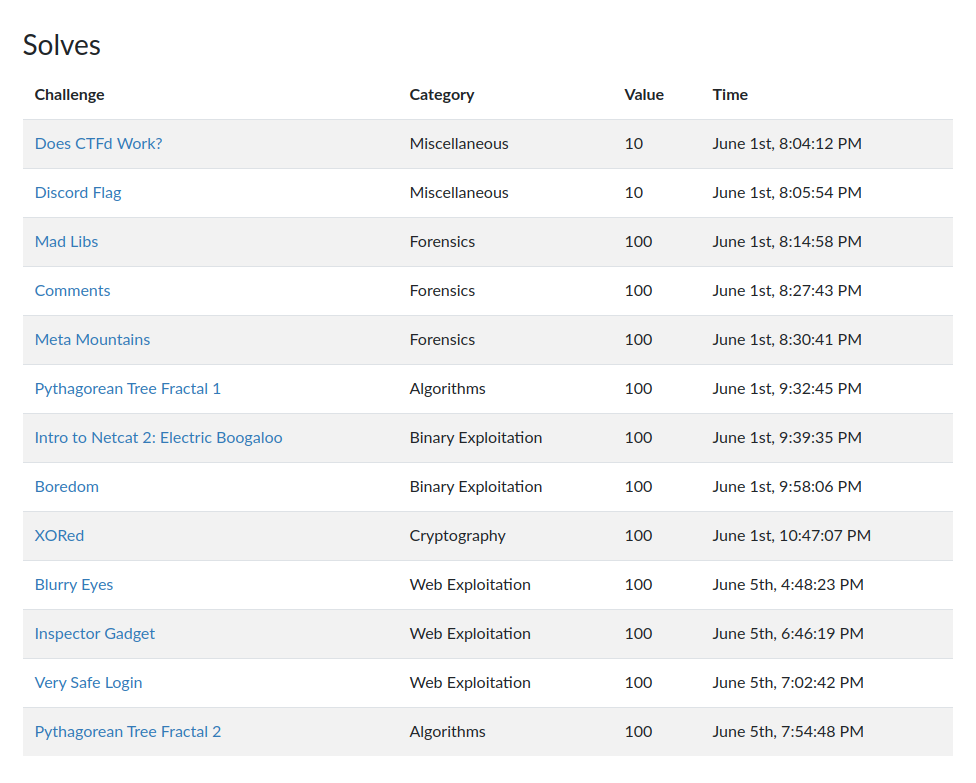
hsctf7_Score2.png



アルゴリズムで解けた２問だけWriteup残しておきます。

[Algorithm]: Pythagorean Tree Fractal 1

Challenge

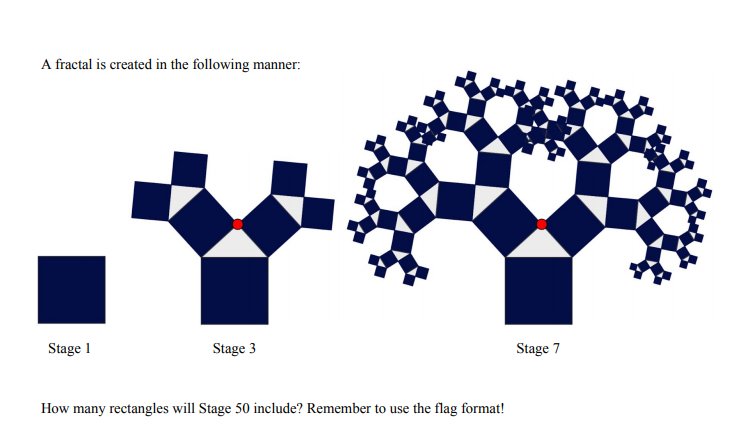
hsctf7_Algo1.png

Attachment:

  • Pythagorean_Tree_Fractal.pdf (中身は上の通りです)


Solution

傾向を確認します。

1: 1個
2: 3個
3: 7個
4: 15個

正方形の合計の数は、こんな感じで増えていきます。

数式にすると、a[n]=2^n-1

（これは、“1 3 7 15"とかでググっても見つかります。）


50番目は、以下の通りです。

$ Python3
>>> 2**50-1
1125899906842623


Flag: flag{1125899906842623}





[Algorithm]: Pythagorean Tree Fractal 2

Challenge

If the square in Stage 1 has an area of 70368744177664, what is the area of the Stage 25 tree?

Attachment:

  • PTF2.pdf (図の部分はPythagorean Tree Fractal 1と同じです)


Solution

70368744177664は、2^46 です。

2個目の正方形の面積は、ピタゴラスの定理とか使って考えると、結果的に (1個目の面積 / 2) になります。

ということで、面積だけ見ていくと、以下の傾向となります。

1: 2^46
2: 2^45
3: 2^44
4: 2^43
5: 2^42

正方形の数は、以下のように増えていきます。（サイズ毎の数で、合計ではないです）

1: 1個
2: 2個
3: 4個
4: 8個
5: 16個


以下のコードを書きました。

1
2
3
4
5
6
7

#!/usr/bin/env python3
# -*- coding: utf-8 -*-
total = 0
for i in range(0,25):
    area = 2**(46-i)
    total = total + area * (2**i)
print(total)


Flag: flag{1759218604441600}